Here we give a few details regarding the ollggamma package that we developed (package here).

Note that the source code can be found in the GitHub repository.

Formulas

The Odd Log-Logistic Generalized Gamma (OLL-GG) [1] distribution is generated by applying a transformation upon the GG cumulative distribution, thus defining a new cdf F(t) as follows: $$ F(t) = \frac{G(t)^\lambda}{G(t)^\lambda - (1 - G(t))^\lambda } $$ where $G(t)$ is the cdf for the GG distribution (which is given later), and $\lambda$ is the new parameter introduced by this transformation.

The probability density function is then: $$ f(t) = \frac{ \lambda g(t) { G(t) (1 - G(t)) }^{\lambda - 1} }{ { G(t)^\lambda + [ 1 + G(t) ]^\lambda }^2 } $$ where g(t) is the pdf for the GG distribution.

The quantile function is: $$ F^{-1}(q) = G^{-1}\bigg( \frac{ q^{1/\lambda} }{ (1 - q)^{1/\lambda} + q^{1/\lambda} } \bigg) $$ where $G^{-1}$ is the GG quantile function.

The generalized gamma distribution proposed by Stacy [2] has parameters $a, d, p$, but here we adopt the reparametrization $$ a = a $$ $$ b = p $$ $$ k = \frac{d}{p} $$ as is used by the R package ggamma.

Probability density function $$ f(x) = \frac{b x^{bk-1} \exp[-(x/a)^b]}{a^{bk} \Gamma(k)} $$

Cumulative density function $$ F(x) = \frac{\gamma(k, (x/a)^b)}{\Gamma(k)} $$

Deriving the quantile function is not trivial, but is discussed in the ggamma page.

A Few Plots

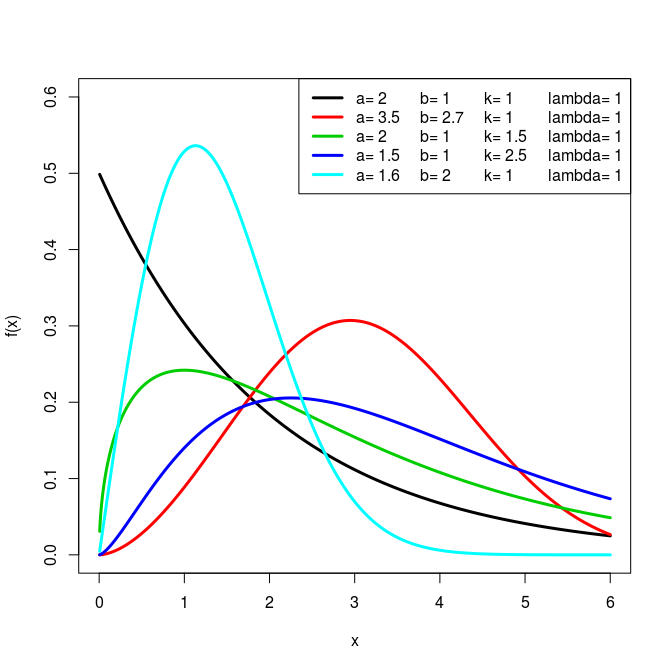
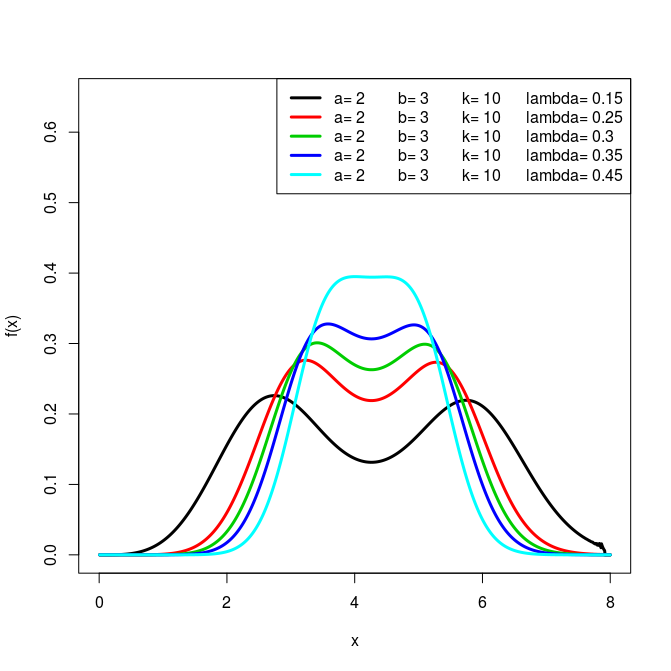
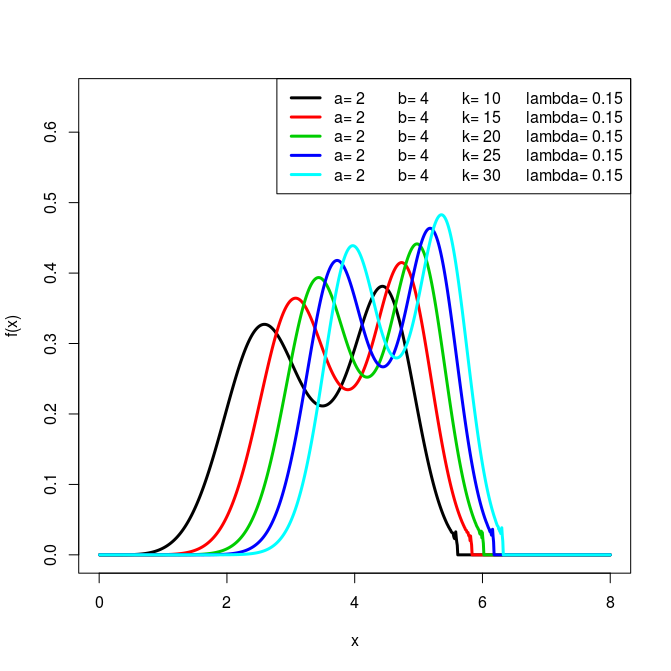
References

[1] - Prataviera, F., Cordeiro, G. M., Suzuki, A. K., & Ortega, E. M. M. (2017). The odd log-logistic generalized gamma model: properties, applications, classical and bayesian approach. Biom Biostat Int J, 6(4), 00174.

[2] - Stacy, E. W. (1962). A generalization of the gamma distribution. The Annals of mathematical statistics, 33(3), 1187-1192.